Discrete Time System

The difference equation for an Infinite Impulse Response (IIR) filter is
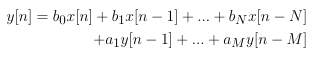
It defines the relationship between the input and output of the filter: the n^th output y[n] is a linear combination of the corresponding input x[n], the N previous input x[n-1] , ..., x[n-N] and the M previous outputs y[n-1] , ..., x[n-M].

If all a_i coefficients are zero (i>0), it is a Finite Impulse Response (FIR) filter and the b_i coefficients are the impulse response of the filter.
Indeed, in that case, no output y[n-k] is sent back to the input and if all inputs are set to 0 at a given time, all outputs will be zero once the N previsous samples have reached the output. Otherwise, if one a_i is not zero, the output continue to feed the input indefinitely and it is an Infinite Impulse Response (IIR) filter.

The transfer function in the z-domain (z = e^{i ω} = cos(ω) + i sin(ω)) is
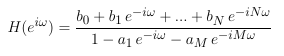
It is the equivalent of the transfer function in the Laplace domain resulting of the discretization (sampling) of the system. If in the Laplace (continuous) domain, frequency range is [ 0 , ∞ ], In the z-transform domain, it is [ 0, 2 π]. The relation between f in the frequency domain and ω in the z-domain is ω = 2 π f / Sample Rate.

The transfer function in the Laplace domain can be written as
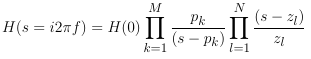
where the p_k and z_j are the M poles and N zeros of the transfer function.